快速排序

快速排序我们一般将其简称为快排, 是一种非常高效的算法，时间复杂度O(nlogn), 空间复杂度为O(1), 是一种不稳定的原地排序算法。 JavaScript中sort函数的实现就用到了快排，源码如下， 710行起， 大概是当排序数组的长度小于等于10时， 使用插入排序， 当大于10时则使用快排。

快排原理

给定一个数组，假设待排序区间的下标为p到r，我们选择p到r之间的任意一个数据作为pivot(分区点)，遍历p到r， 将小于pivot的放在左边，大于pivot的放在右边。经过这一步骤，数组p到r之间的数据就被分为了三部分，假设目前pivot所在位置下标为q, 则p到q - 1的为小于pivot的，中间是pivot，以及 q + 1 到r的为大于pivot的。之后递归处理p到q-1和q+1到r之间的数据，当区间缩小为1时，所有的数据就都有序了。

我们以8、10、2、3、6、1、5数组为例，以最后一个数据5作为pivot，第一次分区之后如下排列

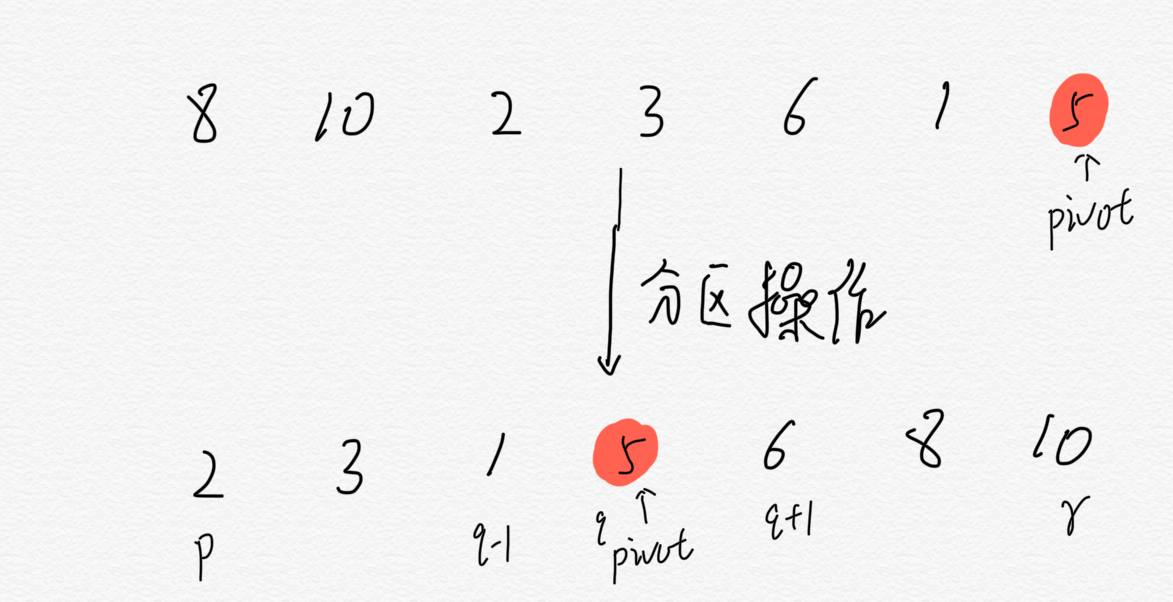
第一次分区的过程如下

代码实现

用JavaScript代码实现如下

function quick_sort(nums) {
  let len = nums.length
  if(len <= 1) return nums

  quick_sort_c(nums, 0, len - 1)

  return nums
}
// 快速排序递归调用函数
function quick_sort_c(nums, p, r) {
  if(p >= r) return

  // 获取分区点
  let q = partition(nums, p, r)
  console.log(q)
  quick_sort_c(nums, p, q - 1)
  quick_sort_c(nums, q + 1, r)
}
function partition(nums, p, r) {
  let pivot = nums[r]
  let i = p
  for(let j = p; j < r; j++) {
    if(nums[j] < pivot) {
      // 交换nums[i] 和nums[j] 且 i++
      let tmp = nums[i]
      nums[i] = nums[j]
      nums[j] = tmp
      i++
    }
  }
  let tmp = nums[i]
  nums[i] = nums[r]
  nums[r] = tmp
  return i
}
let nums = [4,5,6,1,2,3,23,44]
console.log(quick_sort(nums))

拓展：如何利用快排找到数组中第K大元素

我们假设有一个数组A， 我们选择A[0, n-1]的最后一个元素A[n-1]作为pivot， 对数组A进行原地分区，这样，我们就可以得到三部分A[0, p - 1], A[p], A[p + 1, n - 1], 当p + 1 === K时， 那么 A[p]即为即为要查找的元素， 如果 p + 1 > k, 那么查找的元素就在A[0] ~ A[p - 1]之间，反之，则在 A[p + 1] ~ A[n - 1]之间，之后，在相应的区间之内递归查找， 直到满足 p + 1 === K，此时说明直到了。